Estoy seguro de que la gran mayoría de los que terminan la secundaria, encuentran en el tema de razonamiento o habilidad matemática sólo un apoyo para obtener más aciertos en su examen de ingreso.
En este CONAMAT post quiero mostrarte que el Razonamiento Matemático no es un tema más en el examen de ingreso al bachillerato, sino que es todo un curso formal en matemáticas y para ello, te mostrare problemas cuya solución está llena de creatividad y belleza en sus operaciones, como son los que se resuelven con Razonamiento Inductivo.
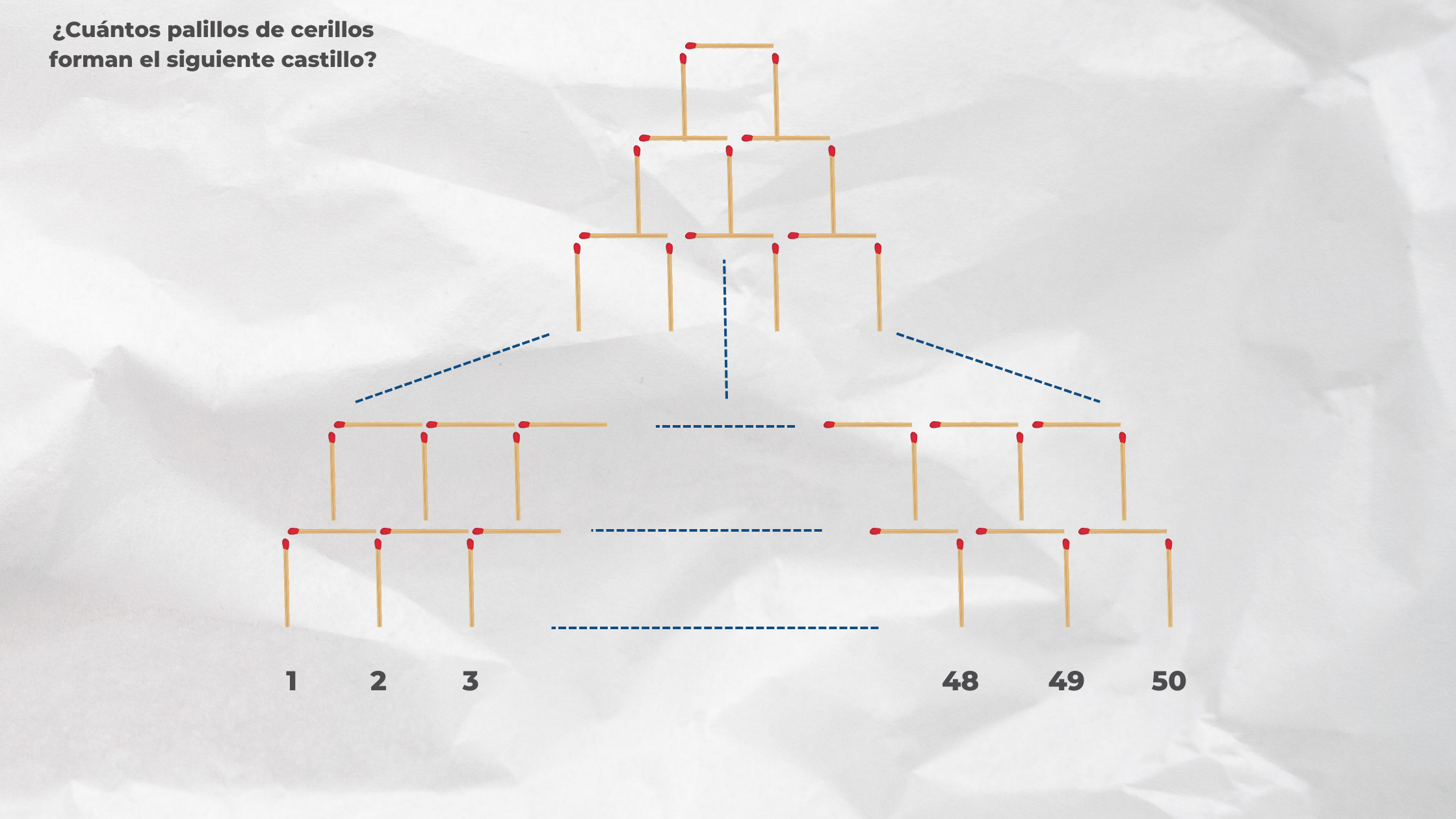 Arreglo con palillos de cerillos
Arreglo con palillos de cerillosPara resolver el problema su solución está dada por el Razonamiento Inductivo, el cuál será nuestro tema de estudio y al final podrás resolverlo tú mismo.
Es un procedimiento de análisis de casos particulares, es decir, casos pequeños que ayudan a descubrir de los resultados propiedades que se cumplen en ellos y que permiten obtener conclusiones generales.
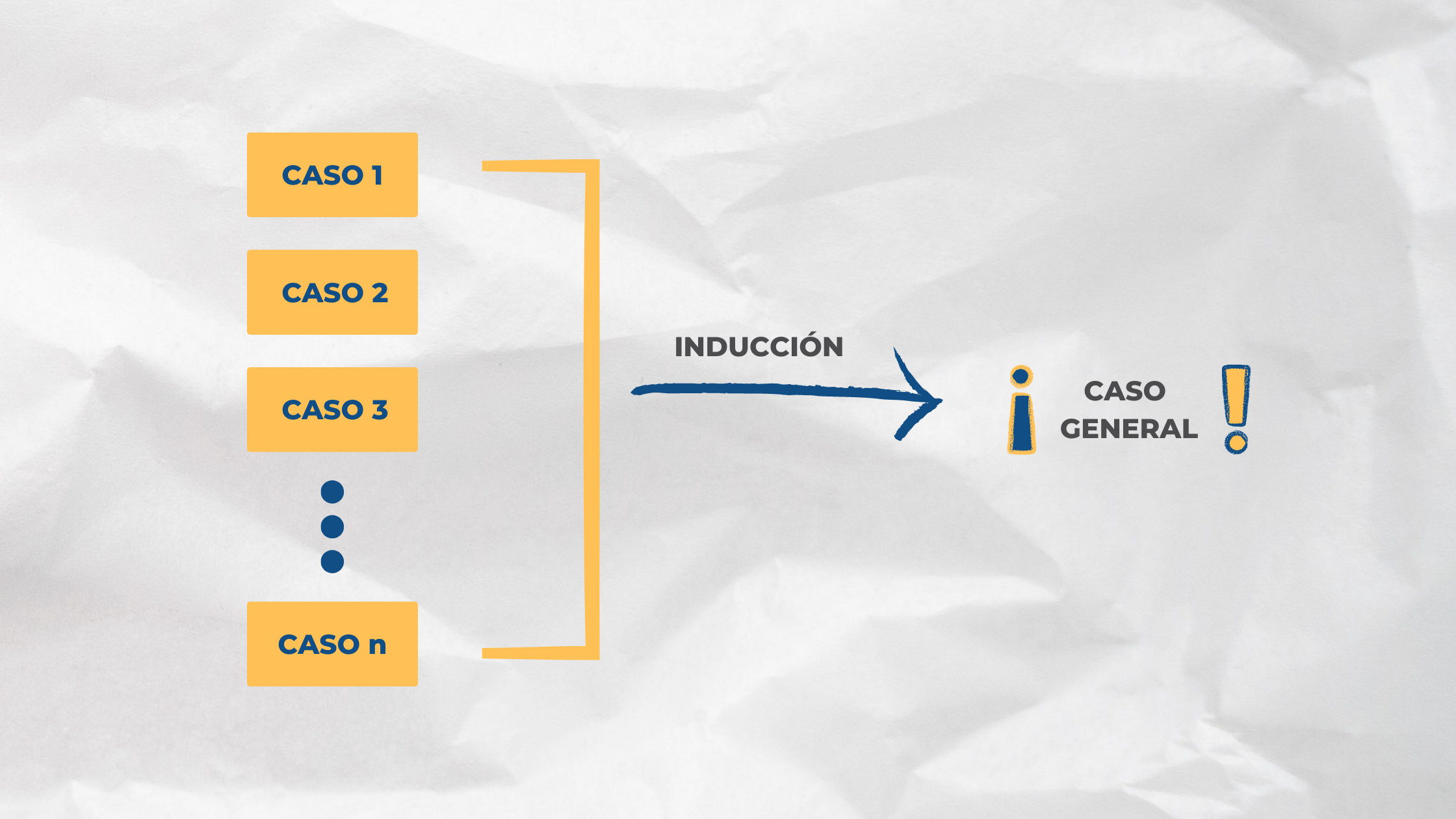 Concepto de Razonamiento Inductivo
Concepto de Razonamiento InductivoPaso 1: Identifica la forma general del problema.
Paso 2: Establecer por lo menos 3 casos para su posterior análisis.
Paso 3: Observar y analizar los 3 casos para llegar a una conclusión general
En los problemas al realizar los casos se tienen que analizar sus resultados para obtener una relación entre estos, para ello, te mostraré algunas relaciones de formación que te pueden ayudar a obtener la conclusión general.
Ejemplo:
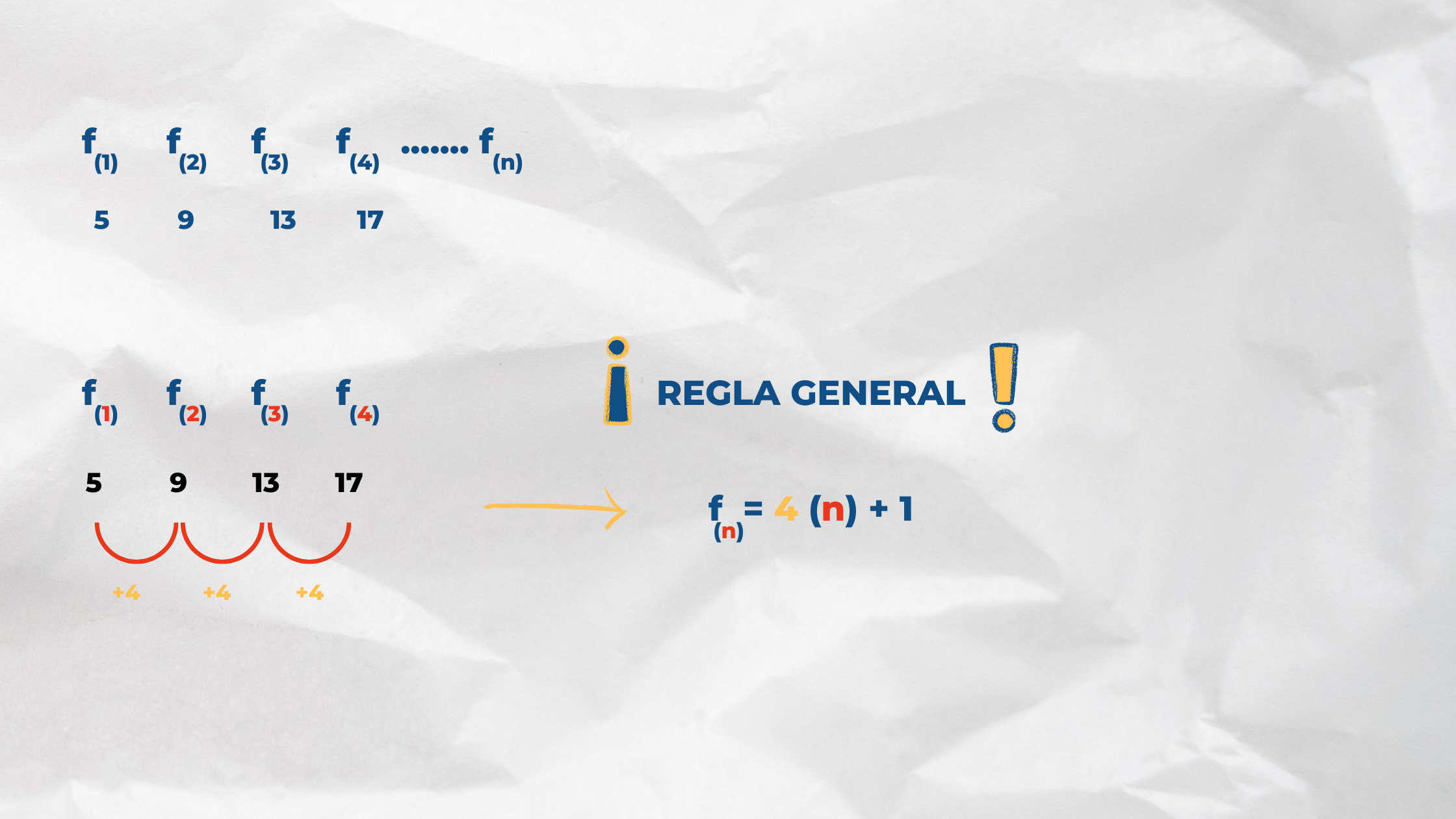
La diferencia entre los términos es 4, los números 1, 2, 3, 4, ... pueden ser "dígitos" o "elementos de las figuras o cifras en los problemas".
Ejemplo:
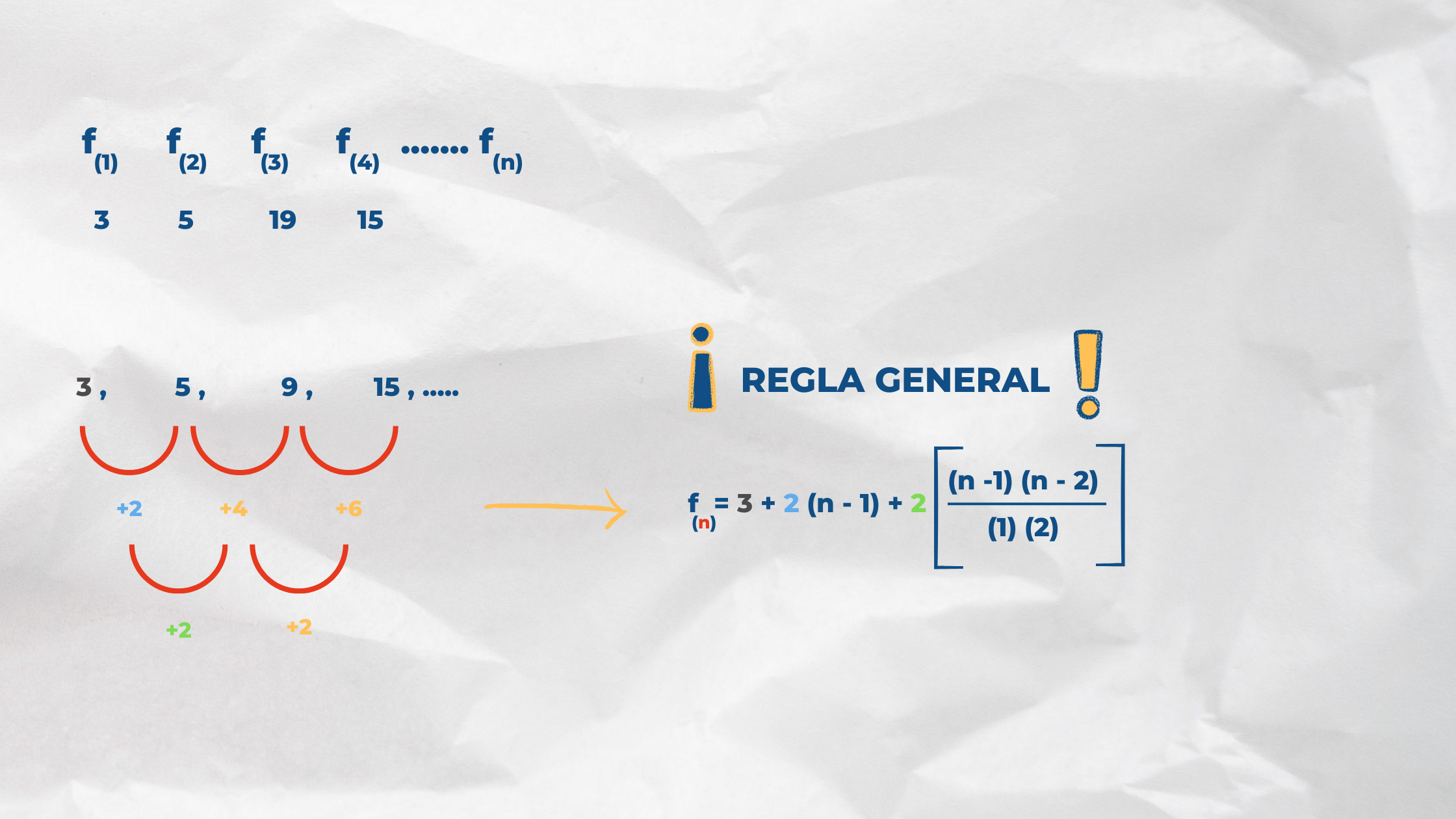
Ejemplo:
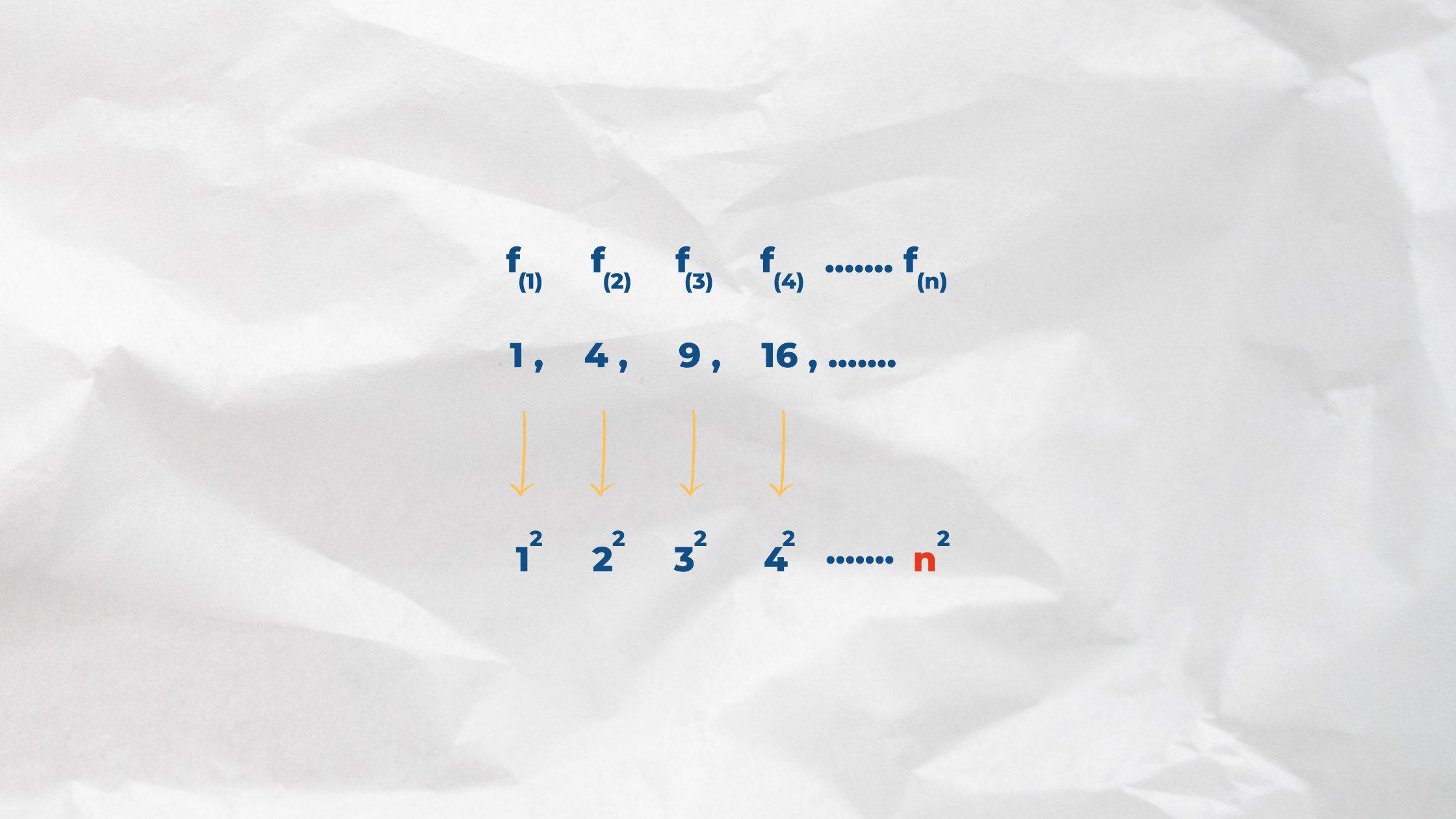
Ejemplo:

Ejemplo:
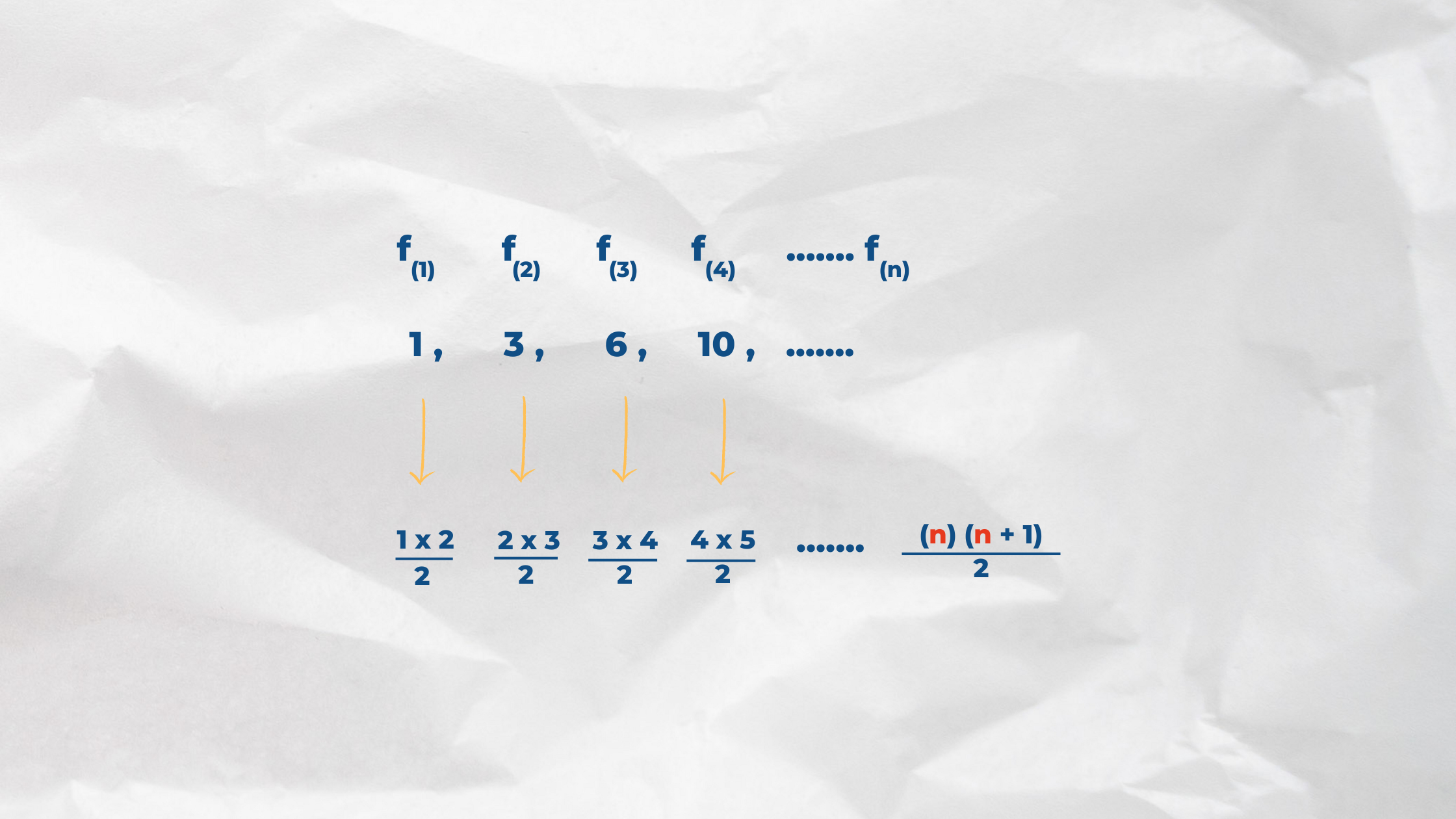
Ejemplo:

En los siguientes ejemplos se muestra la aplicación del razonamiento Inductivo.
Ejemplo 1:
Determina la suma de dígitos del resultado de la siguiente operación.
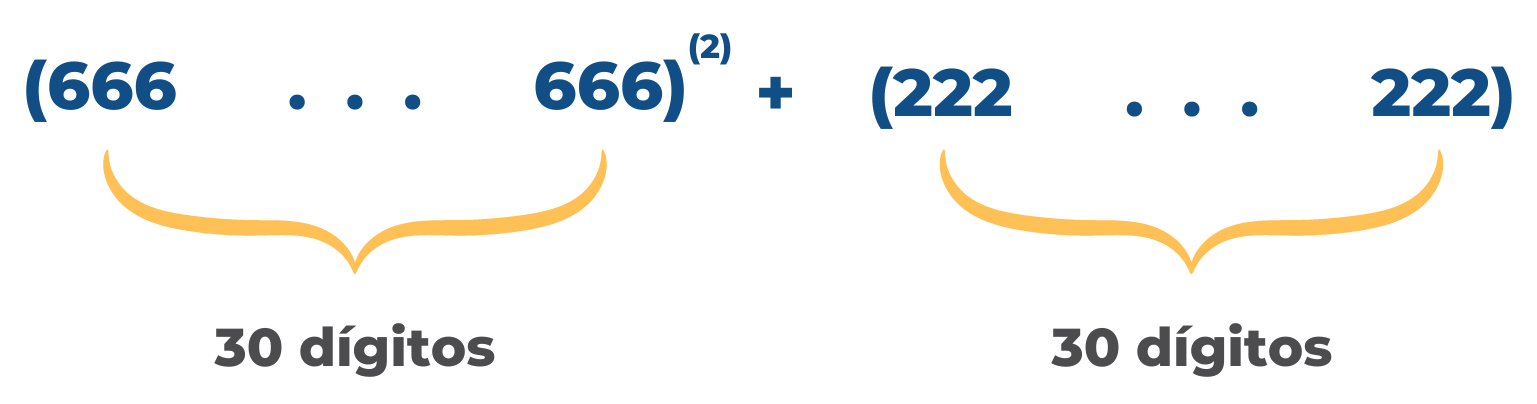 Solución:
Solución:
Se analizan los casos particulares, con base en la siguiente tabla.
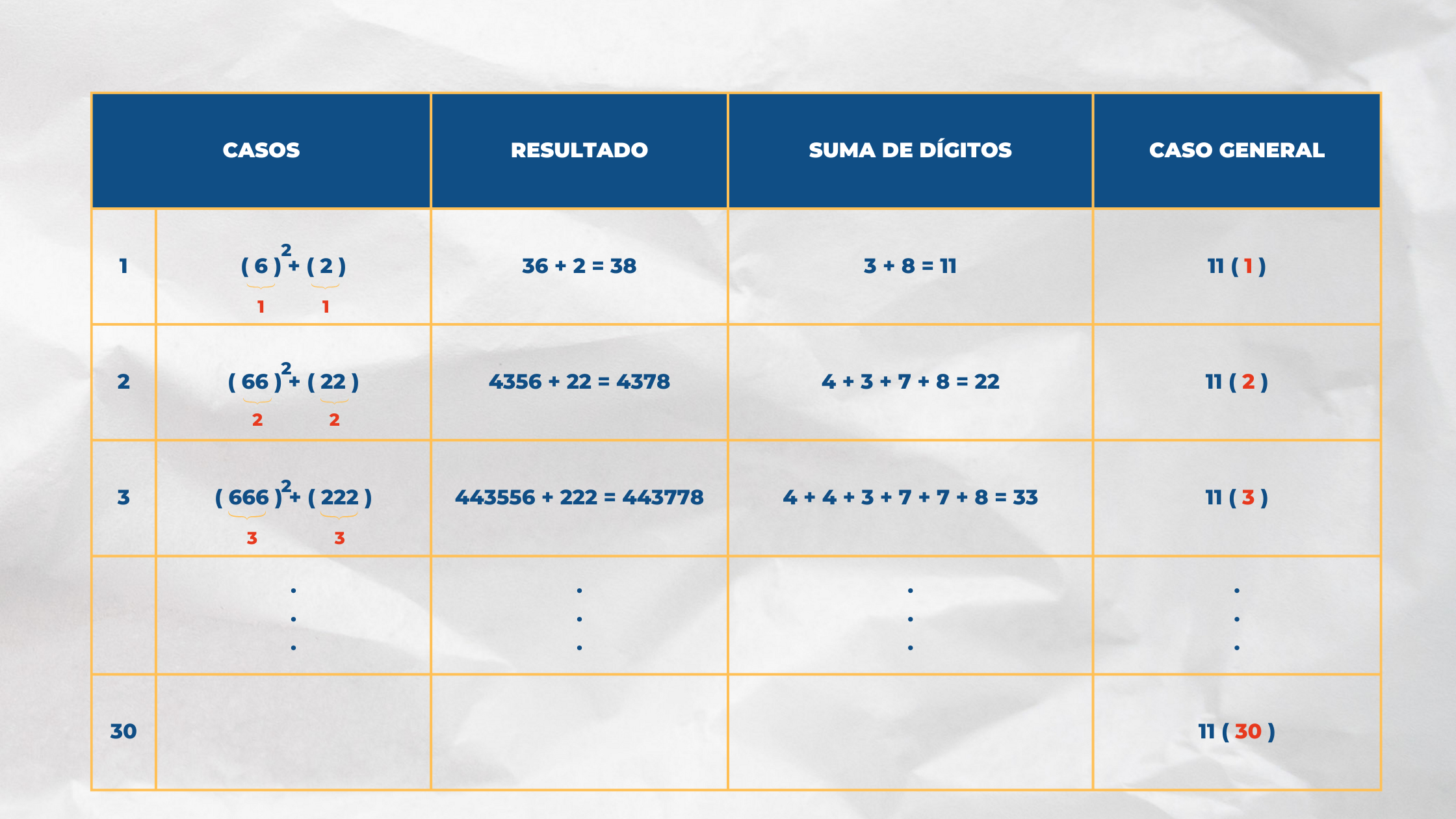
Los números 1, 2, 3, 4, ... representan el número de dígitos de cada operación, entonces, sí se tienen 30 dígitos, por lo tanto, el resultado es 11(30) = 330
Ejemplo 2:
Observa la siguiente secuencia de figuras, con base en ella, determina la suma de todos los elementos de la figura 20.

Solución:
Imagina hacer la figura 5, la figura 6, así hasta la figura 20 con la secuencia de números, esta será muy grande y te llevará mucho tiempo, entonces, para que sea más rápido su solución sin hacer las figuras, es el aplicar el razonamiento inductivo.
Para ello, se toma como mínimo 3 casos:
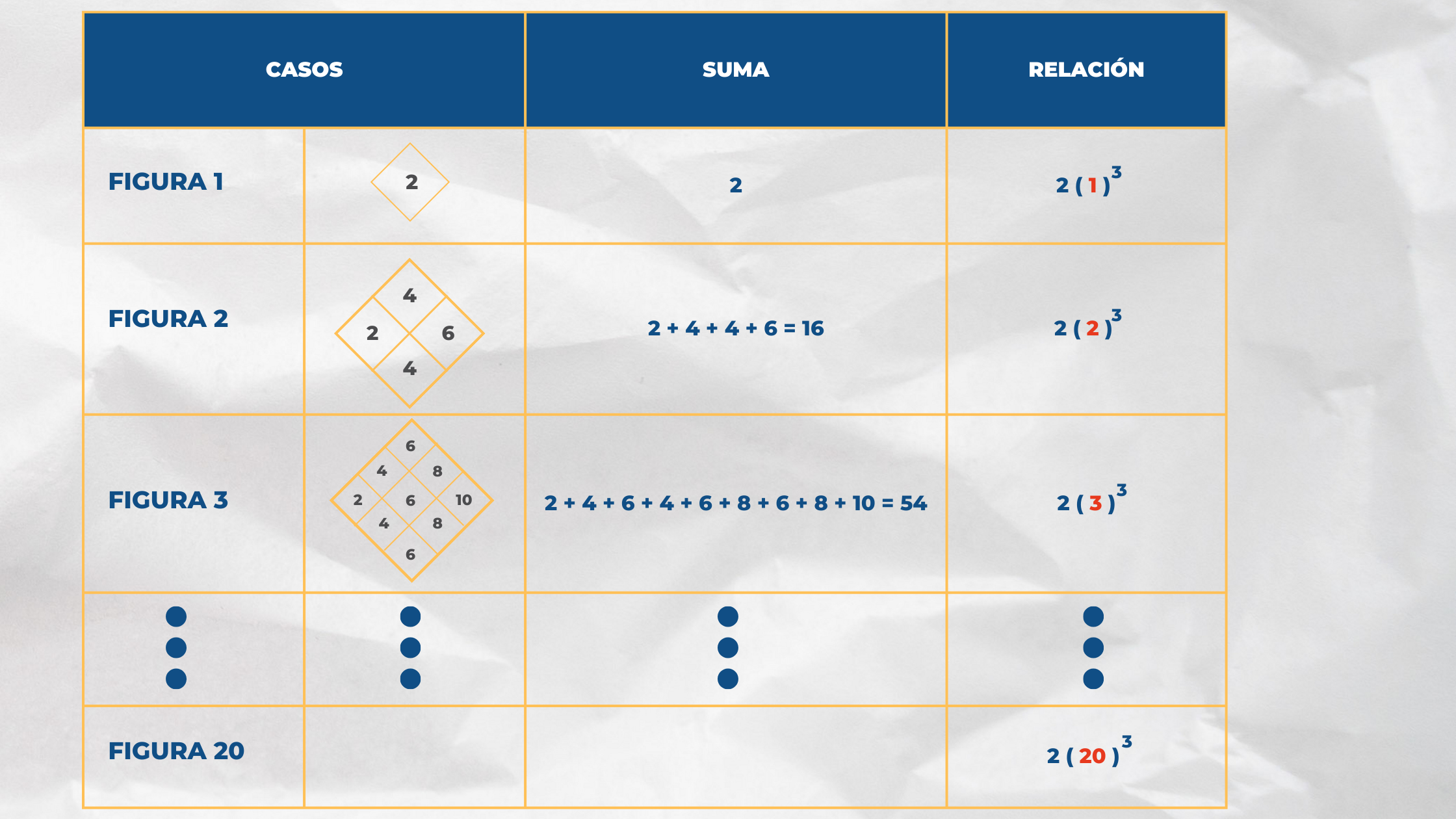
Finalmente, para la figura 20 la suma de sus elementos dará como resultado:
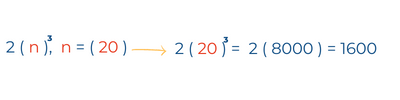
Ejemplo 3:
Sin aplicar calculadora determina el valor de M.
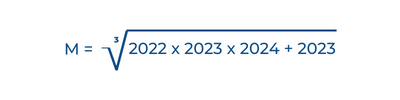
Solución:
Se obtienen los casos particulares. Se observa que en el radicando se encuentra el producto de números consecutivos y se le suma el término central del producto.
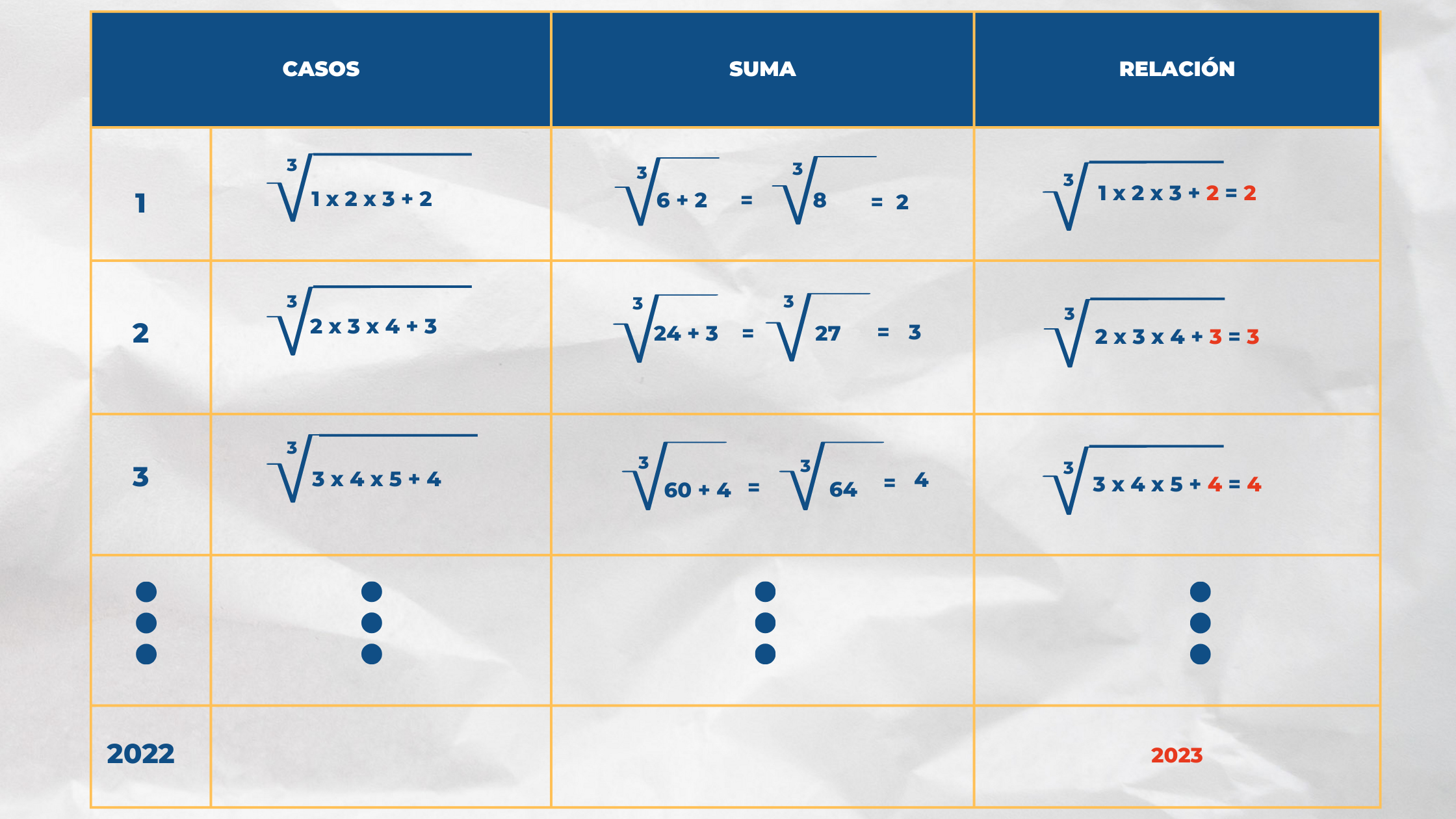
Por consiguiente, el valor de M es 2023
Ejemplo 4:
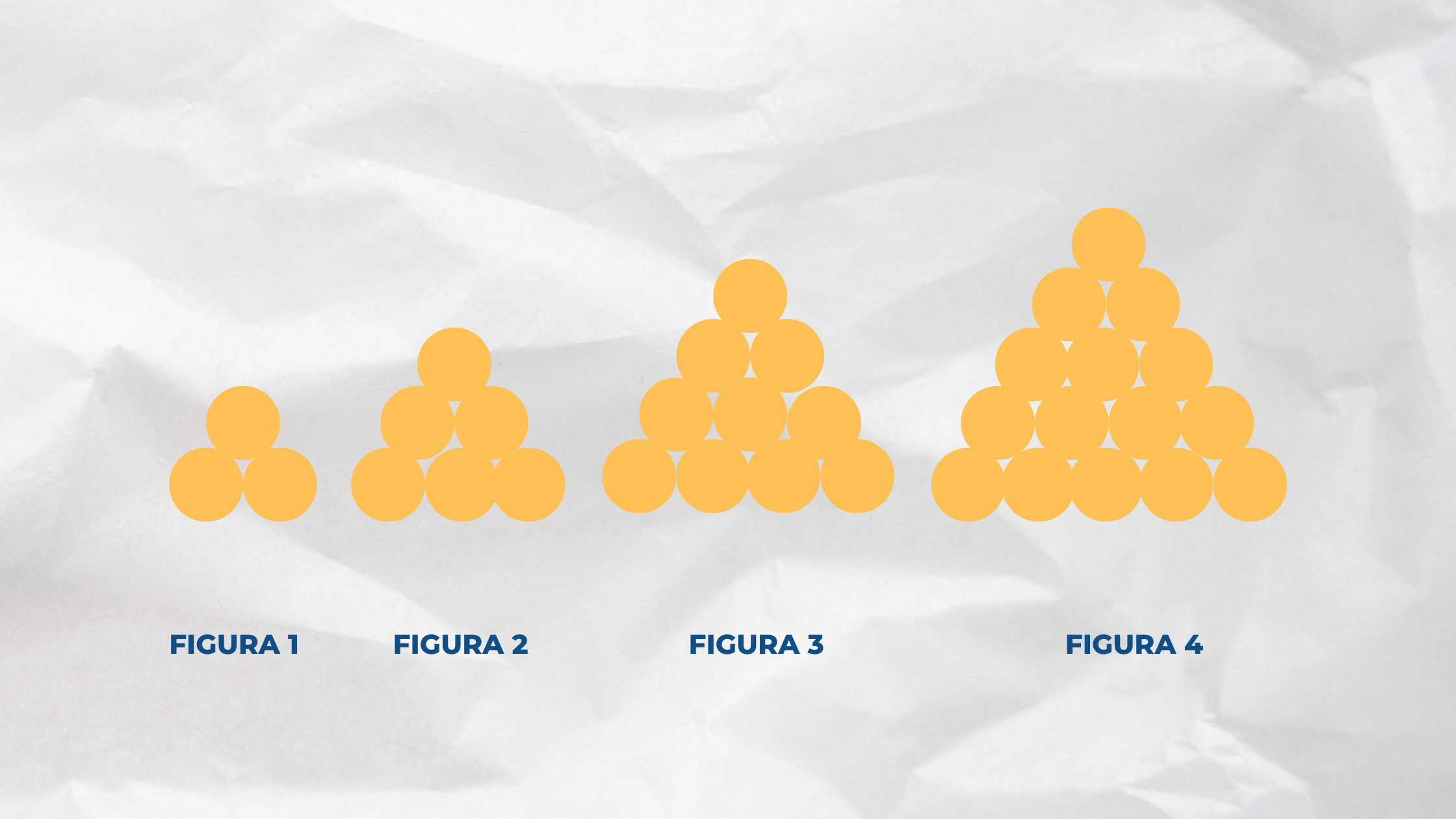
¿Cuántos puntos de contacto habrá en la figura 40?
Solución:
Se cuentan los puntos de contactos en las 3 primeras figuras y aplicando el razonamiento inductivo, obtener el número de contactos que hay en la figura 40.
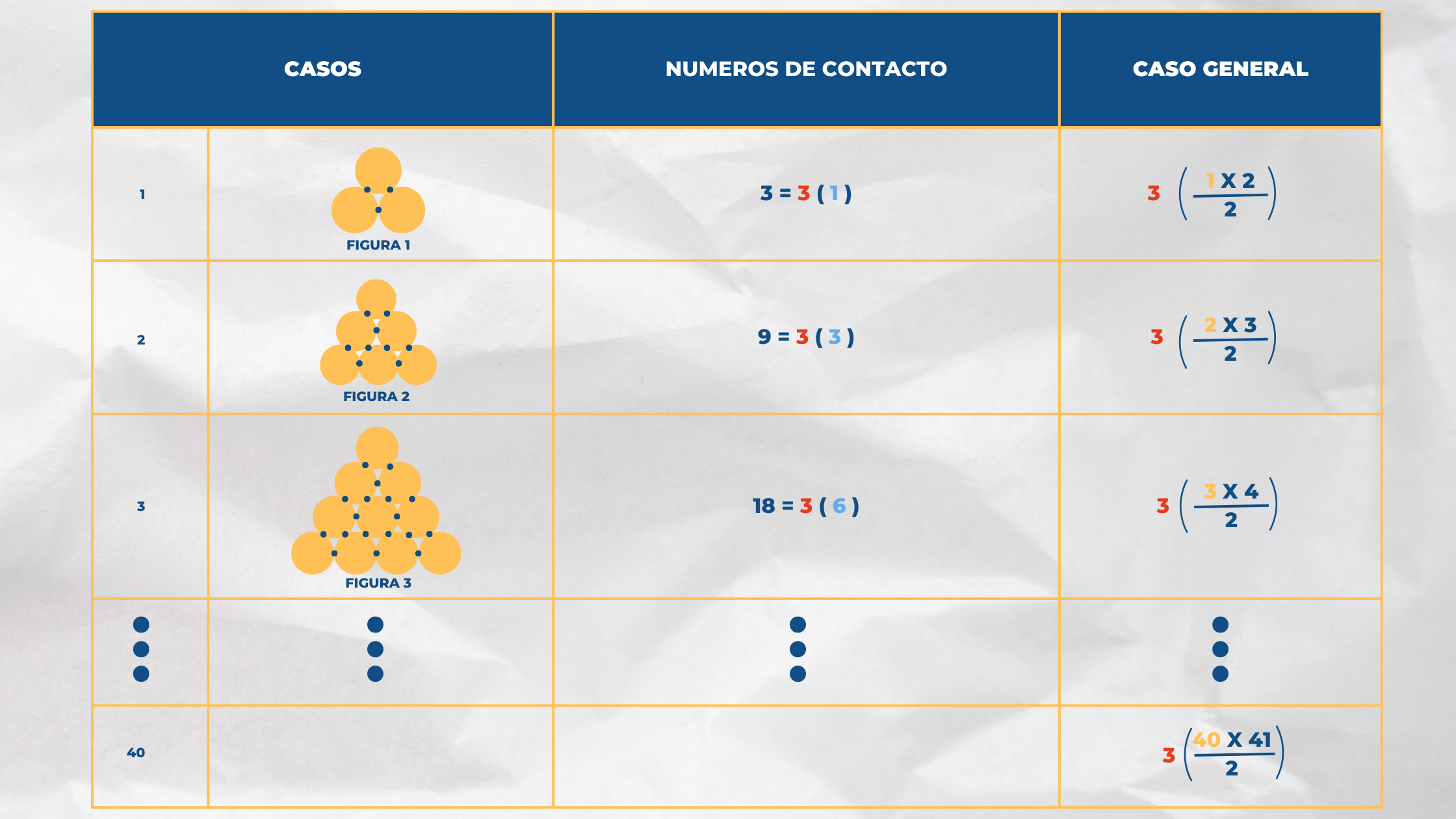
Se observa que los términos 1, 3 y 6 son números triangulares, los cuales tienen su representación.
Por lo tanto, el número de contactos en la figura 40 es:
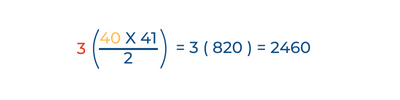
Para terminar este CONAMAT Post te comento que el Razonamiento Matemático te ayuda al desarrollo de cualquier tema de Matemáticas con el apoyo de la Creatividad la cual te da la capacidad de la imaginación y el ingenio para resolver problemas en el mínimo tiempo y esfuerzo.
¡Recuerda que tienen un problema por resolver al inicio de este CONAMT Post y te dejo otro! Sin el uso de calculadora deben obtener el resultado de la siguiente operación:
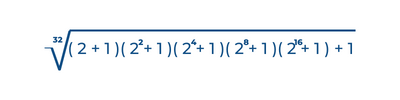
Estas Historias En Matemáticas
Xochicalco 187 Col. Narvarte,
Ciudad de México, C.P. 03020
Llámanos: 800 68 500 50
Email: info@conamat.com
¡Queremos escucharte!
Escríbenos un comentario