Casi en todas los centros educativos de nuestro querido México, en los niveles de secundaria y bachillerato, los profesores nos enseñan a resolver reactivos y problemas de aplicación sobre triángulos rectángulos cuando se proporcionan como datos la longitud de los catetos e hipotenusa, empleando la expresión matemática que se conoce como “Teorema de Pitágoras”.

Hoy vas a aprender otras cosas muy interesantes de esta bella expresión, como es el obtener:
“Ternas pitagóricas” e importantes resultados inspirados en el teorema que se conoce como “Relaciones métricas del triángulo Rectángulo”
Para ello, primeramente, conoceremos un poco de la vida de nuestro protagonista.
 Pitágoras
PitágorasPitágoras, es uno de los personajes de la historia más conocidos, fue matemático, filósofo. Vivió entre los años 580 a.C y 495 a.C. Realizó aportaciones en la astronomía, la música, la filosofía y las matemáticas.
Nació en la Isla de Samos, como su papá era mercader estuvo viviendo en varios lugares que visitaba acompañando a su padre. En el año 535 a.C estuvo en Egipto, ahí estudió geometría, lo que le valió para formular su teorema para determinar los lados de un triángulo rectángulo.
Se dice que Pitágoras fue uno de los matemáticos más completos de la historia, algunos lo consideraban un loco por sus misterios, lo que, sí es verdad, es que fue el primero en establecer la relación entre la música y las matemáticas, formulando las leyes de la armonía, creando la escala musical.
También, se metió mucho a creencias religiosas y fundó una sociedad secreta en Italia “La escuela Pitagórica”, consideraba que el ser humano había sido creado en armonía, tenía un pensamiento creador, también consideraba que el universo está dividido en 3 partes: “el mundo natural” “el mundo divino” y “mundo humano” y consideraba que el ser humano tiene inteligencia y alma.
Antes de iniciar el tema deja que te mencione algo muy singular del teorema de Pitágoras: las ternas pitagóricas.
Lo siguiente muestra cómo obtener lo que en algunos libros de texto se les conoce como “Ternas pitagóricas”. Y para ello, se auxiliará de los triángulos Pitagóricos.
Son aquellos triángulos rectángulos cuyas longitudes de sus lados son números enteros y cumplen el Teorema de Pitágoras.
Forma 1
Si x > y, con x e y números enteros positivos.
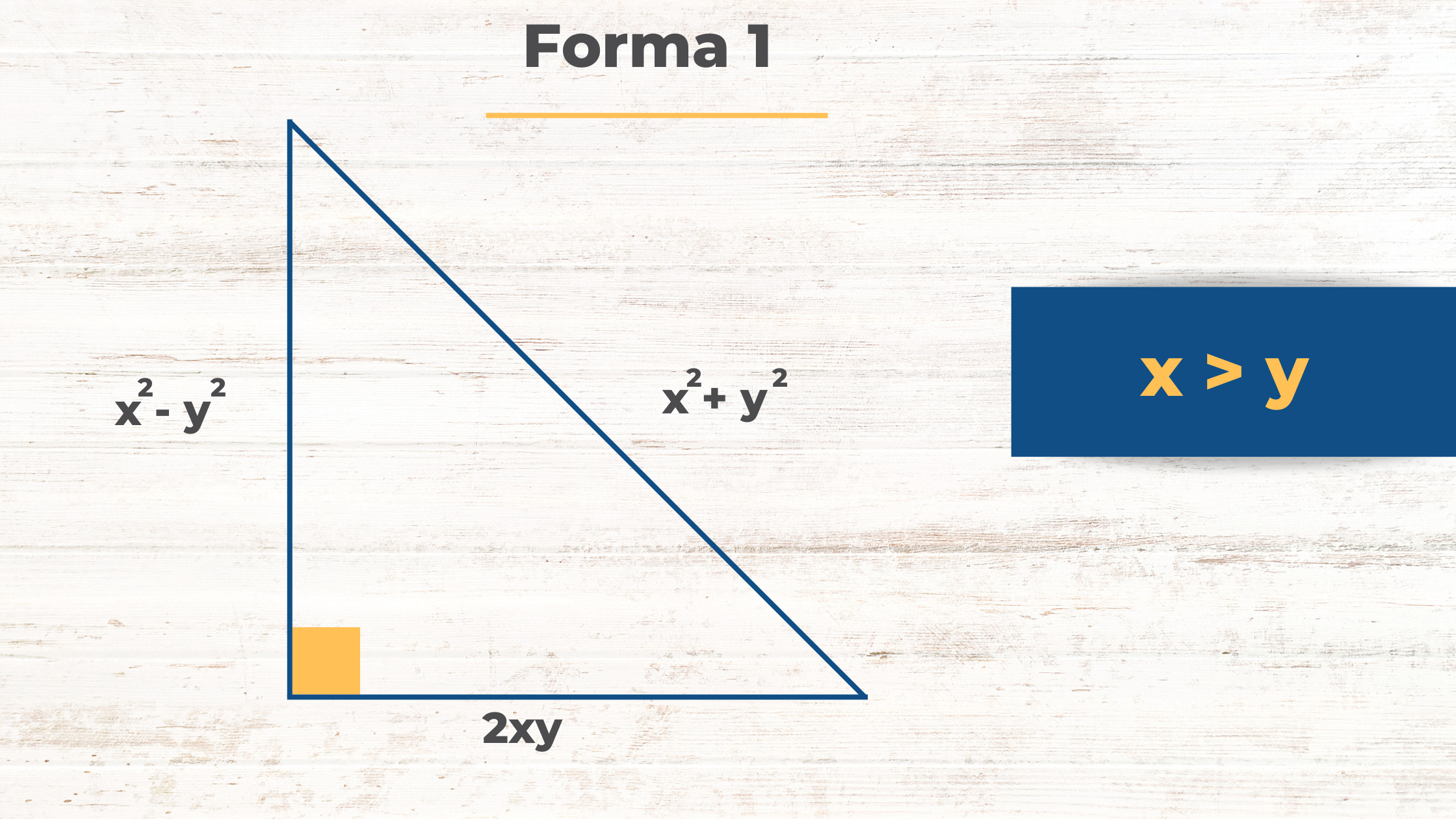 La forma 1 ayuda a obtener ternas pitagóricas dando 2 números enteros positivos
La forma 1 ayuda a obtener ternas pitagóricas dando 2 números enteros positivosEjemplo:

Comprueba que estos valores satisfacen el teorema de Pitágoras.
Forma 2
Si x ≥ 2 y además par.
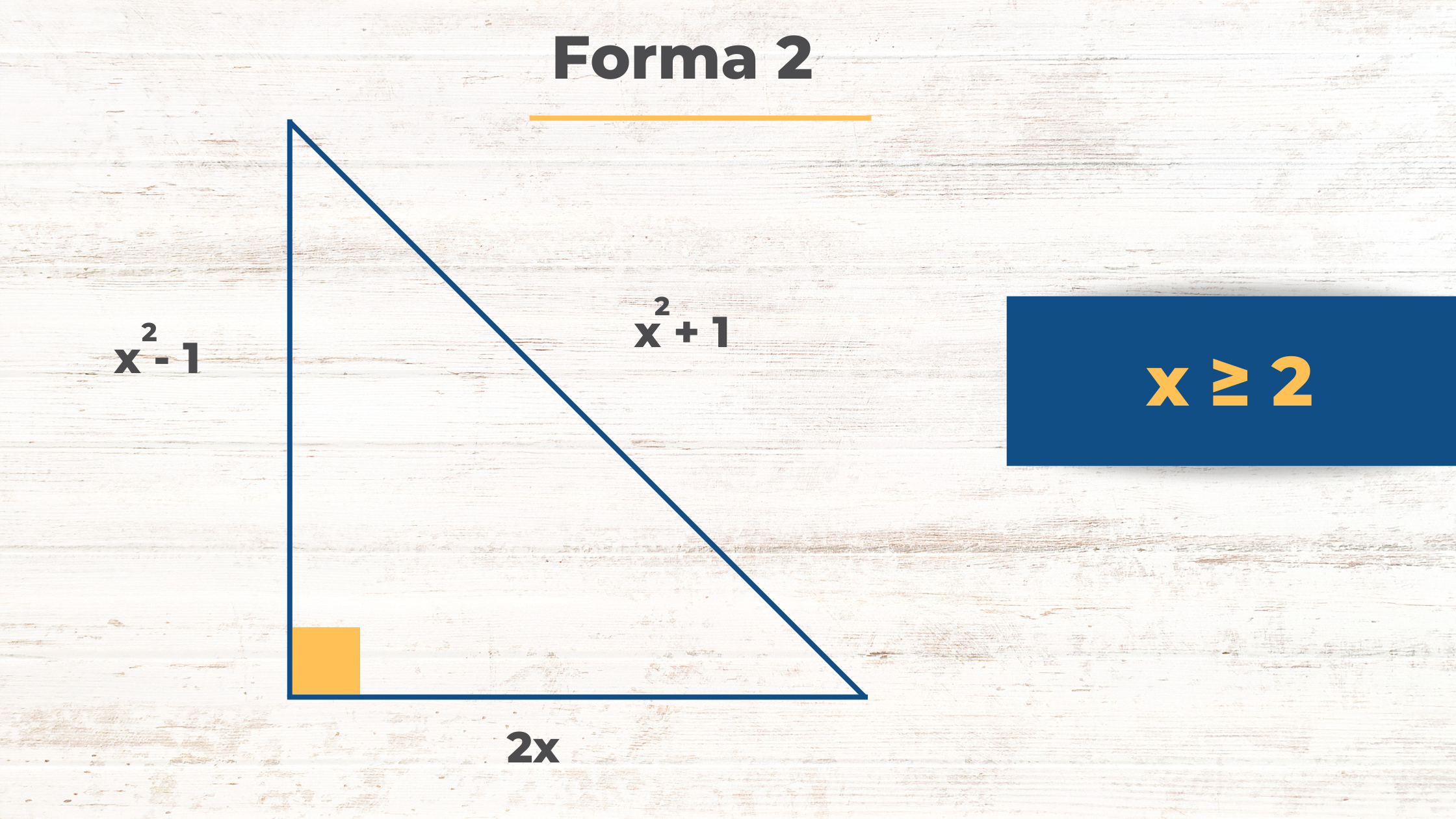 La forma 2 ayuda a obtener ternas pitagóricas dando un números par positivos
La forma 2 ayuda a obtener ternas pitagóricas dando un números par positivosEjemplo

Comprueba que estos valores satisfacen el teorema de Pitágoras.
Forma 3
Si x > 1 y además impar.
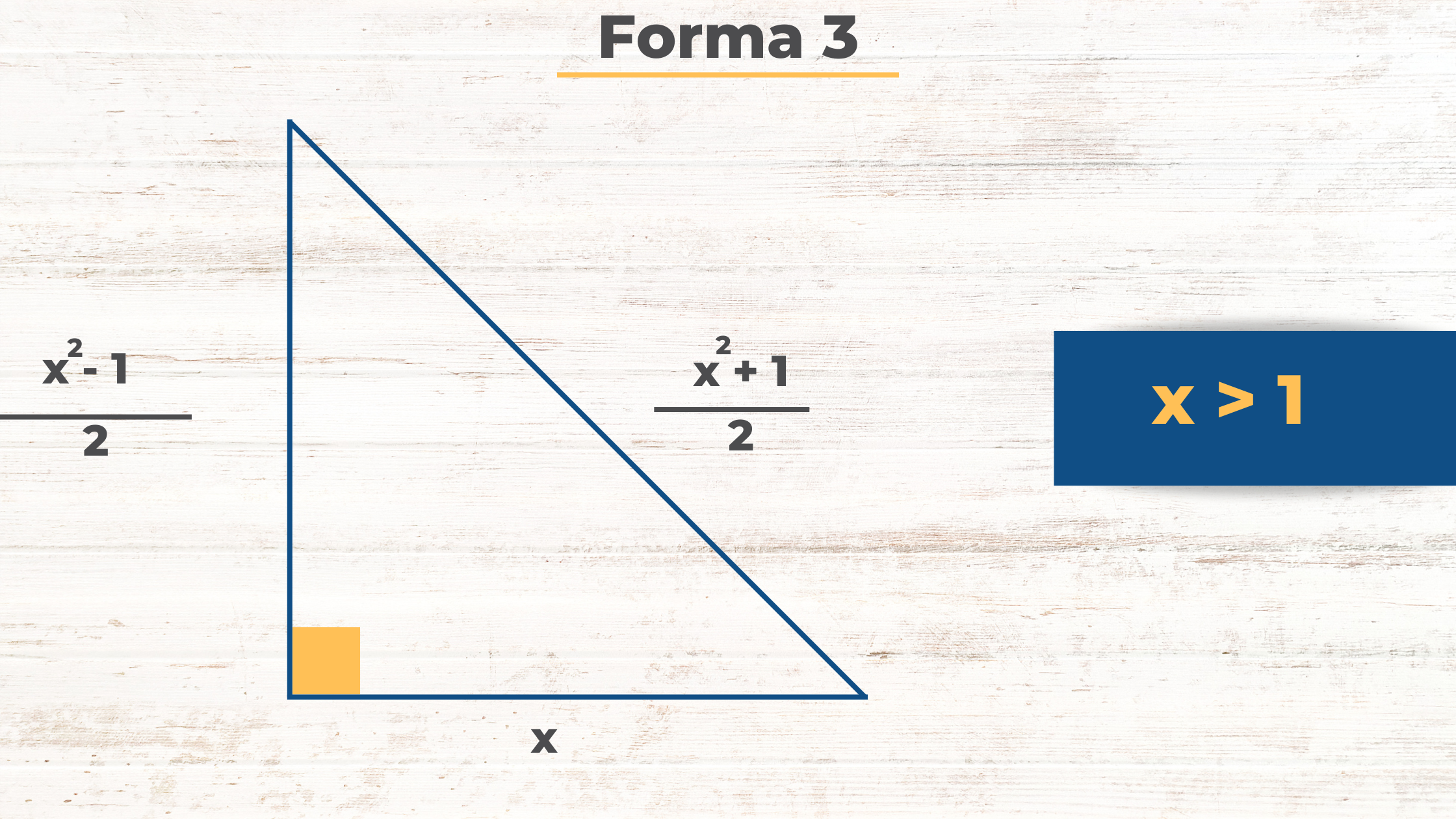
Ejemplo:

Comprueba que estos valores satisfacen el teorema de Pitágoras.
Ahora, después de esta singularidad del teorema de Pitágoras entremos en nuestro tema Relaciones Métricas del Triángulo Rectángulo.
Conceptos básicos.
La proyección ortogonal de un segmento ![]() sobre la recta L es el segmento
sobre la recta L es el segmento ![]() , es decir, el segmento que une los pies de la perpendicular
, es decir, el segmento que une los pies de la perpendicular ![]() sobre la recta L.
sobre la recta L.
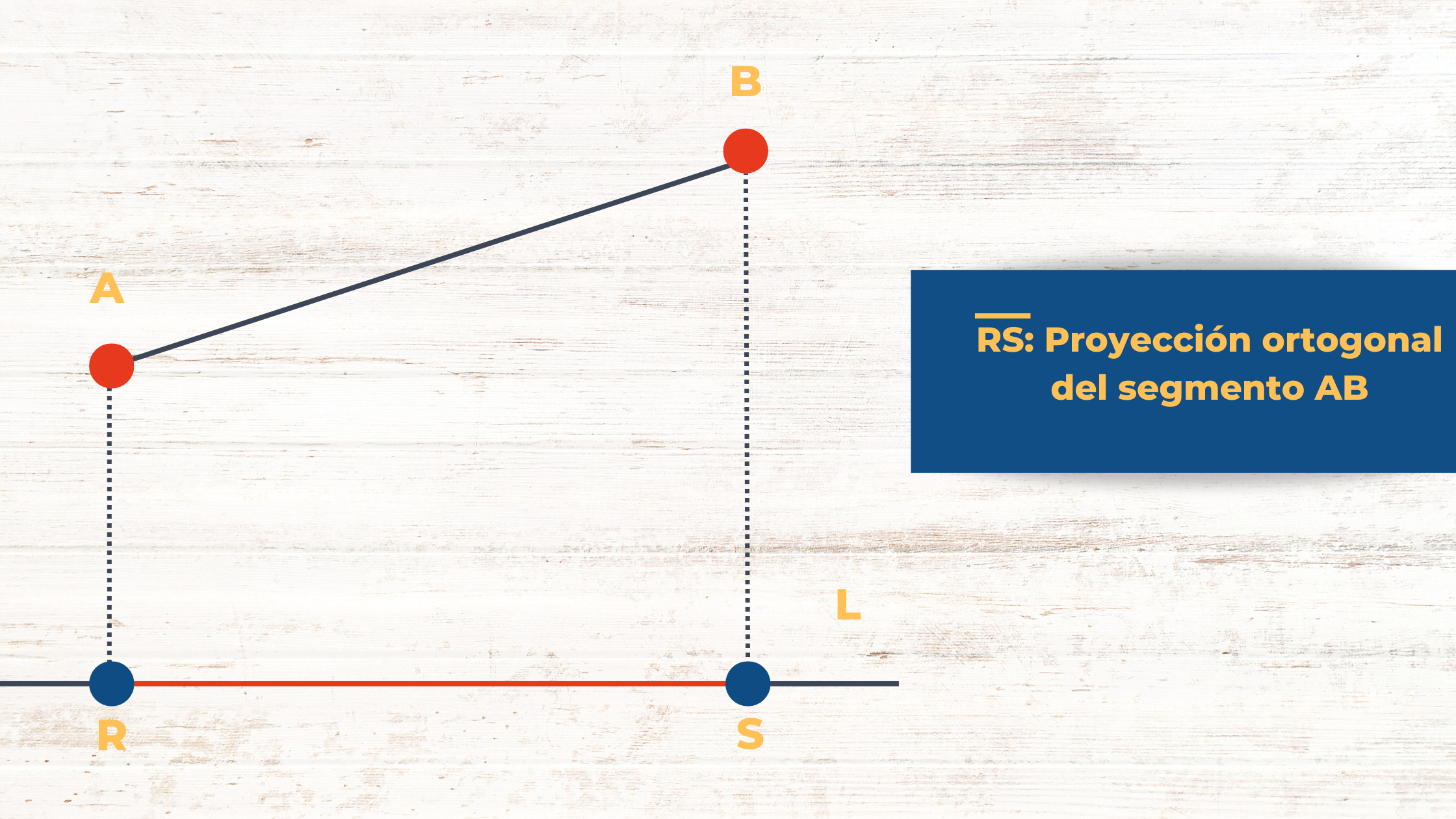 Proyección ortogonal de un segmento sobre una recta.
Proyección ortogonal de un segmento sobre una recta.Teorema del Cateto (Primer Relación Métrica)
En todo triángulo rectángulo, el cuadrado de la longitud de un cateto es siempre igual al producto de la longitud de la hipotenusa y la longitud de su proyección.
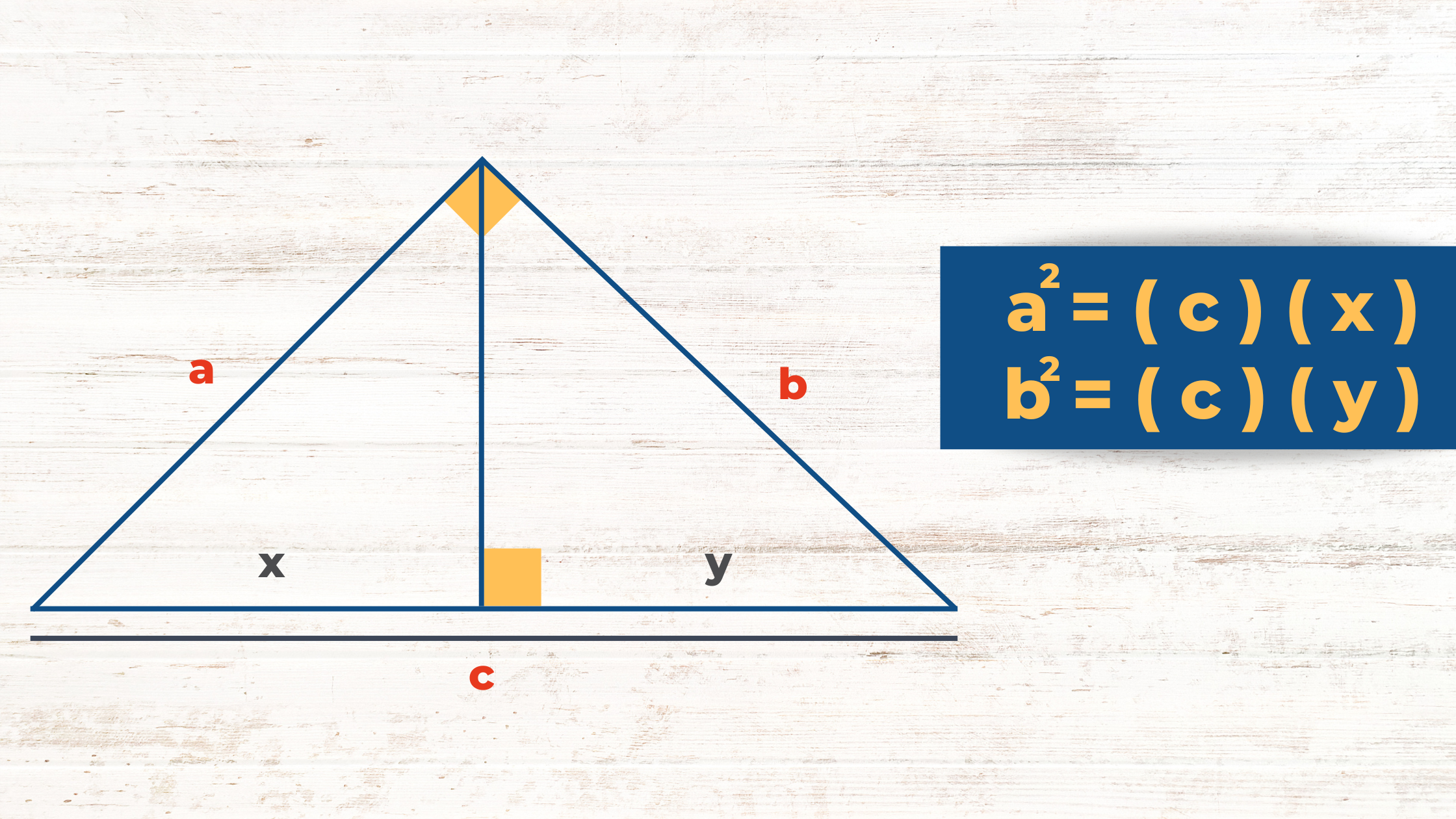 Primer relación métrica.
Primer relación métrica.Si sumas estas expresiones y realizas un poco de álgebra, obtendrás el Teorema de Pitágoras.
Teoremas de la Altura (Segunda Relación Métrica)
En otros libros de texto, encontrarás esta relación métrica como:
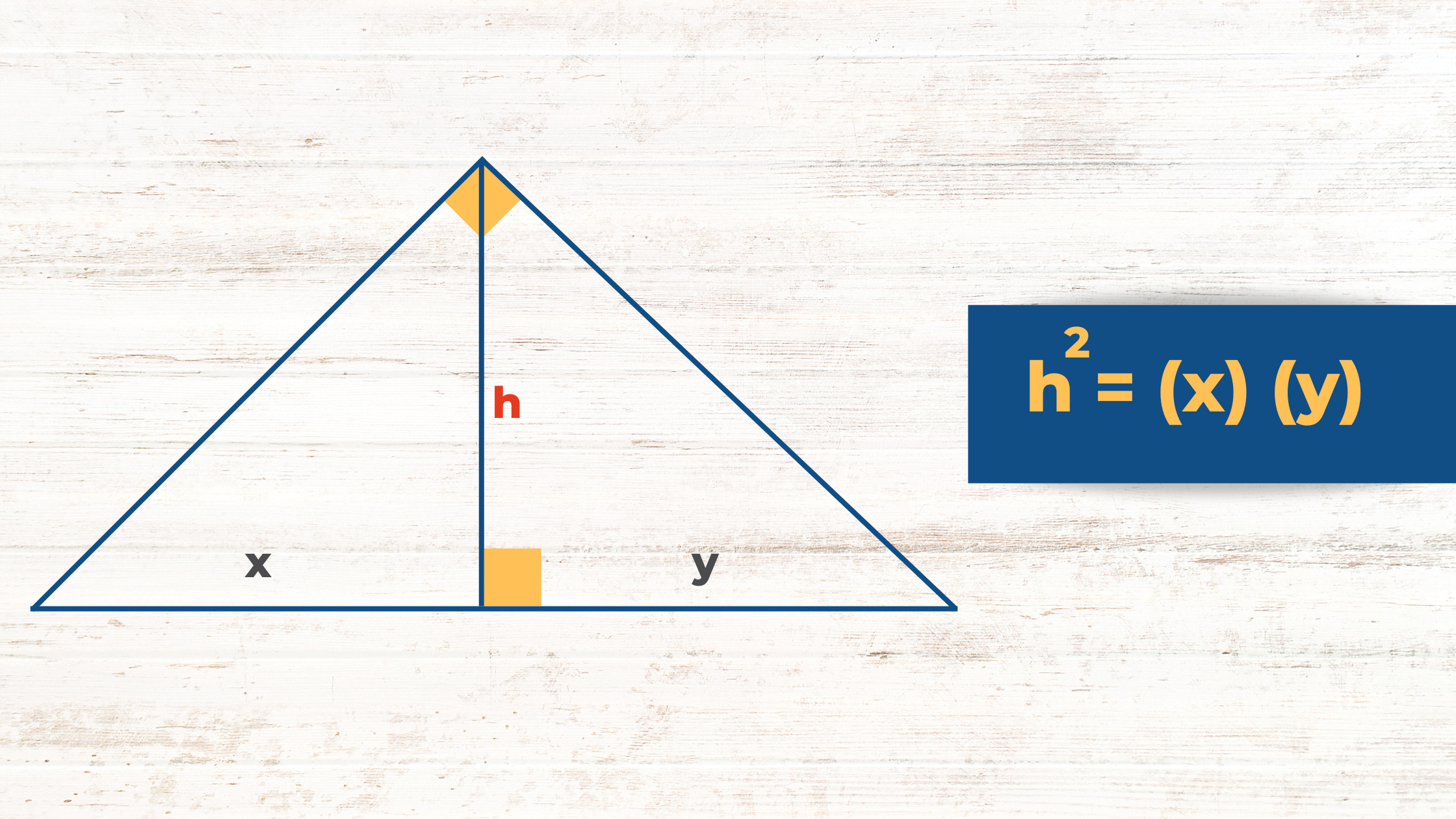 Relación de la altura y la proyección de sus catetos.
Relación de la altura y la proyección de sus catetos.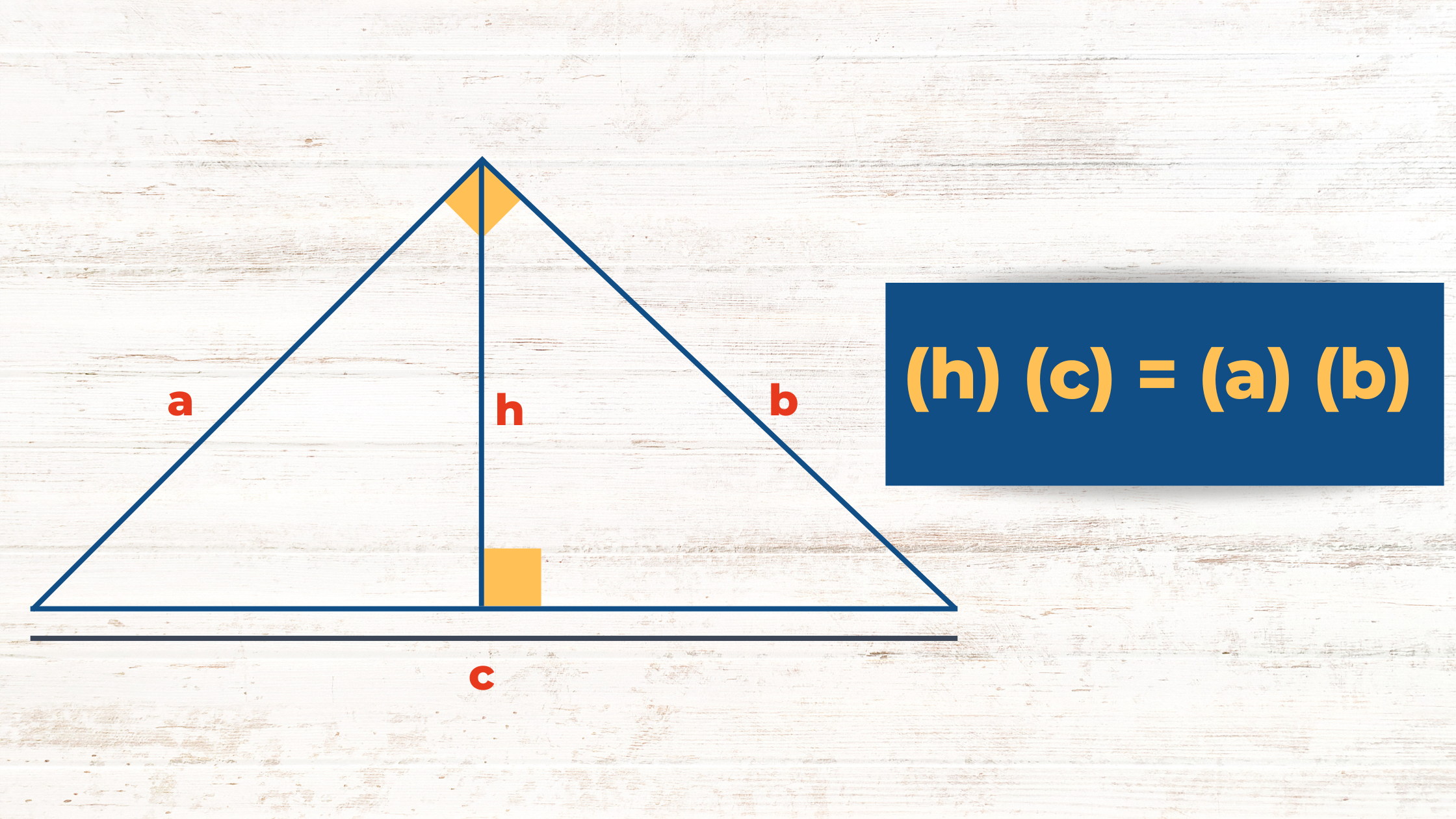 Relación de la altura y los lados del triángulo.
Relación de la altura y los lados del triángulo.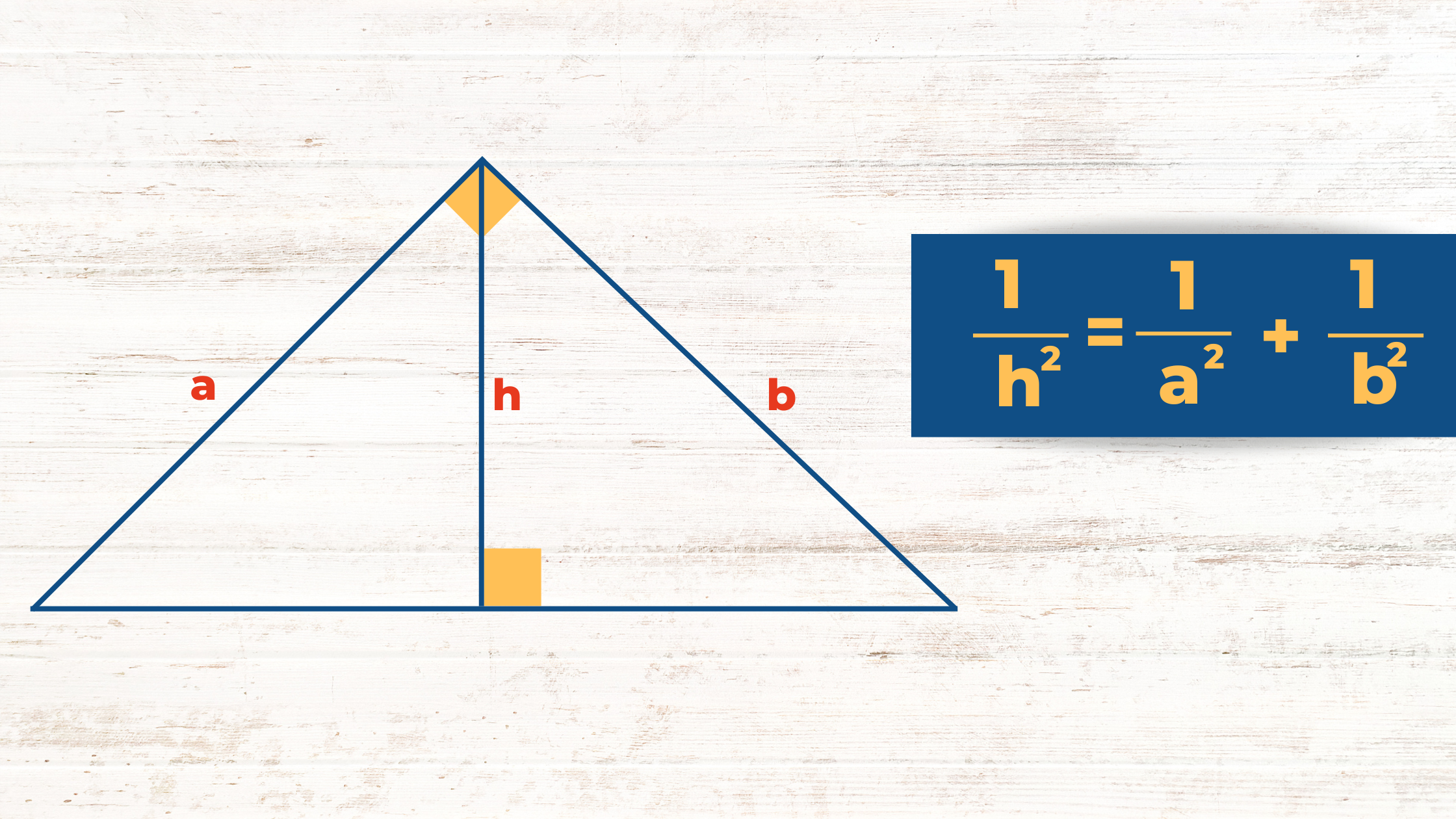 Relación de la altura, sus catetos y el cuadrado de sus recíprocos.
Relación de la altura, sus catetos y el cuadrado de sus recíprocos.Observa la solución del siguiente problema, en el cual se aplica algunas de las relaciones métricas del triángulo rectángulo.
Ejemplo:
Observa la siguiente figura, Sí PQRS un cuadrado, determina la longitud de su lado, se sabe qué ![]() y
y ![]()
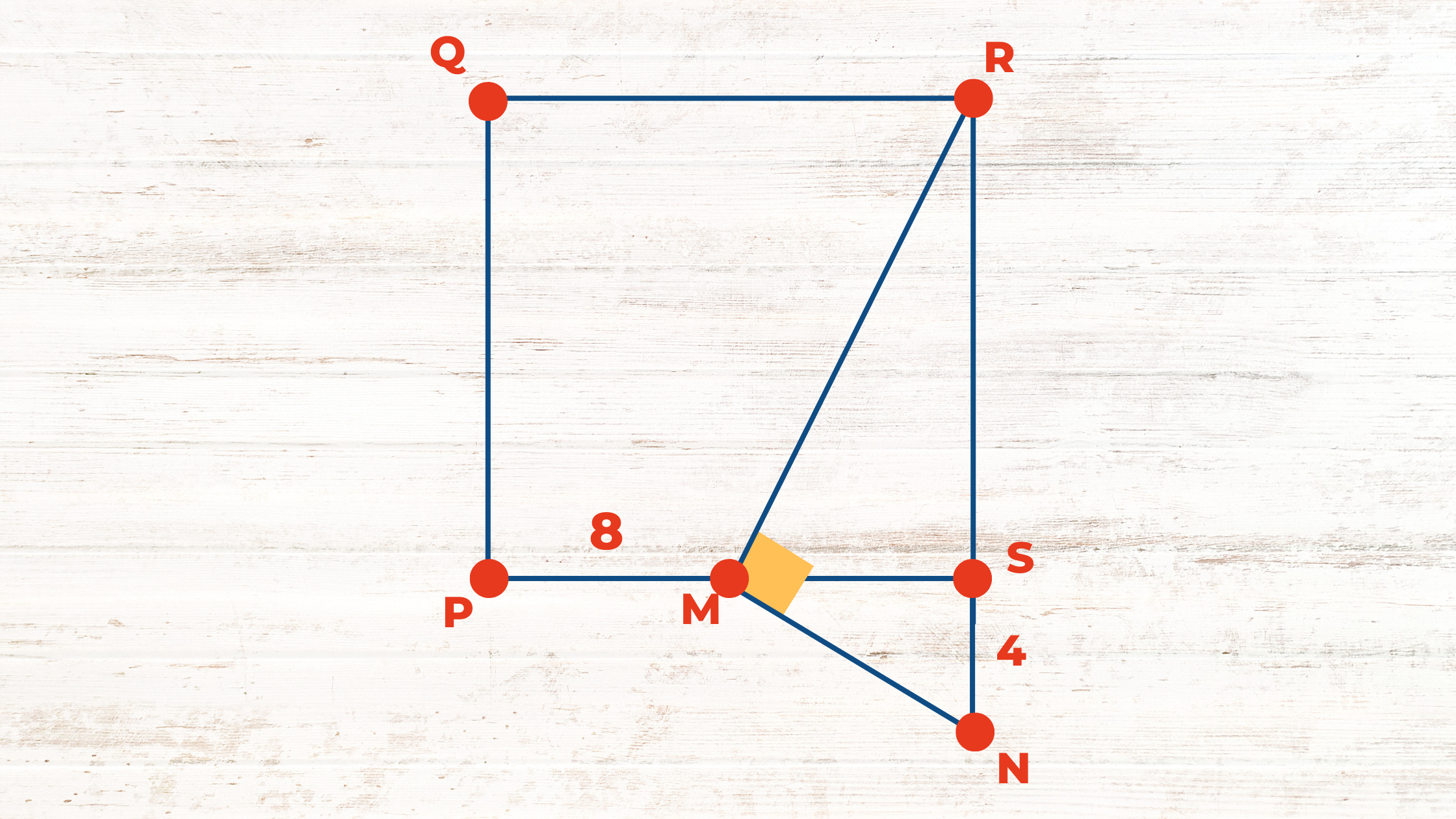
Solución:
De la figura se obtienen los siguientes elementos, como se ejemplifica a continuación:
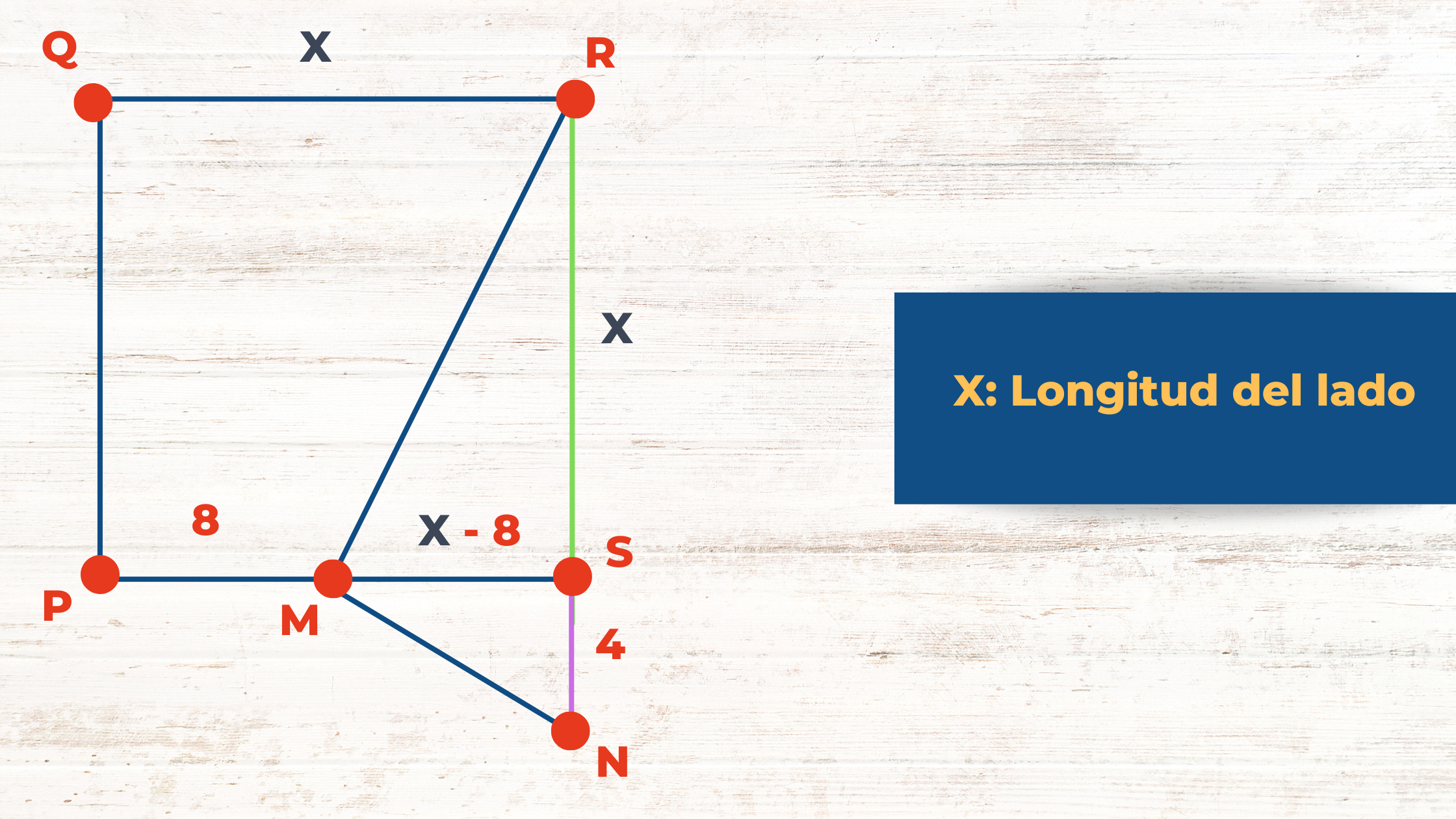
De la figura se observa que el teorema que ayuda a resolver el problema es el primer teorema de las alturas, es decir:

Por lo tanto, la longitud del lado del cuadrado es x = 16.
Para practicar lo aprendido, resuelve el siguiente problema:
Del siguiente triángulo, determina el valor de “x”.
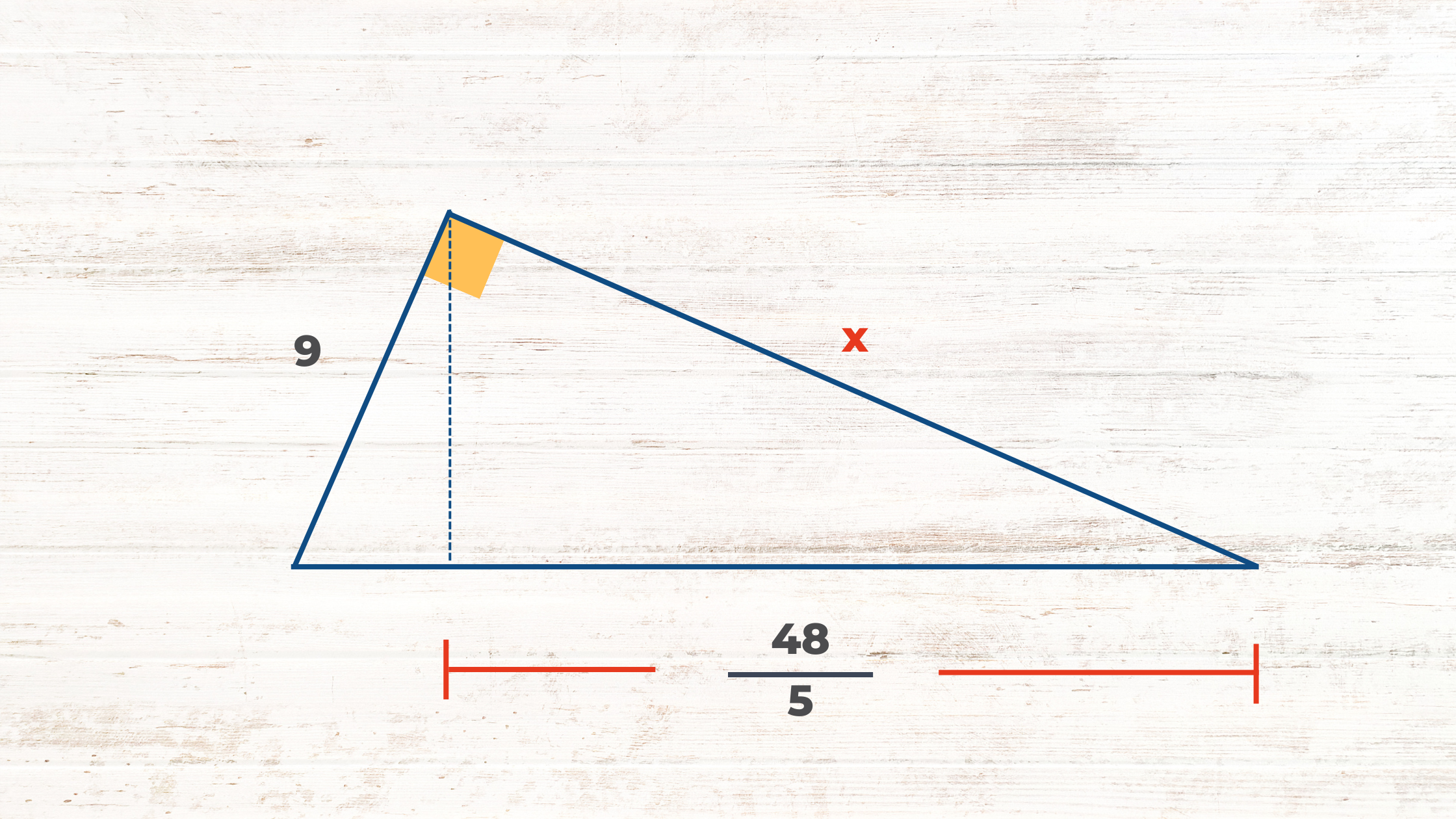
Ahora ya sabes que hay varias propiedades, incluyendo el Teorema de Pitágoras, estas son válidas sólo para triángulos rectángulos y se aplican sobre las longitudes de los catetos, hipotenusa, altura relativa a la hipotenusa y las proyecciones de los catetos sobre la hipotenusa.
Estas Historias En Matemáticas
Xochicalco 187 Col. Narvarte,
Ciudad de México, C.P. 03020
Llámanos: 800 68 500 50
Email: info@conamat.com
¡Queremos escucharte!
Escríbenos un comentario