¿Alguna vez un familiar, un amigo, tu novia o tu novio te ha pedido realizar un reto parecido a este?
Toma esta imagen como referencia e intenta dibujarla sin levantar el lápiz o la pluma del papel y tampoco podrás pasar varias veces por una misma línea.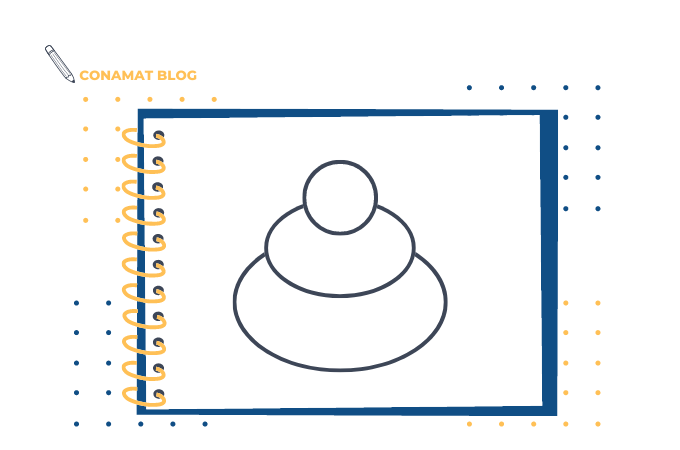
¿Serías capaz de dibujar ahora estas dos figuras sin levantar el lápiz y sin repetir línea?
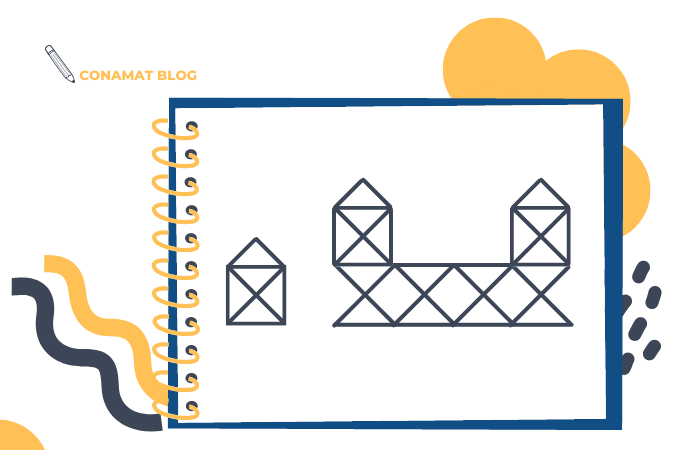
Si no lo lograste, no te preocupes, después de leer nuestro CONAMAT Post sabrás si los retos anteriores se pueden realizar con un solo trazo y el porqué.
Para dar inicio al tema conozcamos un poco de la vida de Leonhard Euler, uno de mis matemáticos favoritos e inspiradores, ya que este personaje es considerado uno de los matemáticos más productivos de la historia y de los más creativos en las áreas de la Matemáticas y la Física.
Nació en Suiza en 1707 en el seno de una familia pobre. Pronto destacó entre el resto de sus compañeros, lo que le permitiría entrar en la universidad a la edad de 13 años, consiguiendo su maestría con tan solo 16 años. Su padre, que era pastor de una iglesia, y su madre, que también era hija de un pastor, querían que Euler se dedicara a la teología, pero, eso no sucedió; ya que Johann Bernoulli, amigo del padre de Euler, se lo llevó a Petersburgo para estudiar Matemáticas.
De las publicaciones de sus trabajos y ensayos se encuentra la colección How Euler Did It. En esta colección podemos descubrir 3 maravillosos trabajos:
Nuestro aprendizaje estará puesto en el tercer trabajo “Los puentes de Königsberg”.
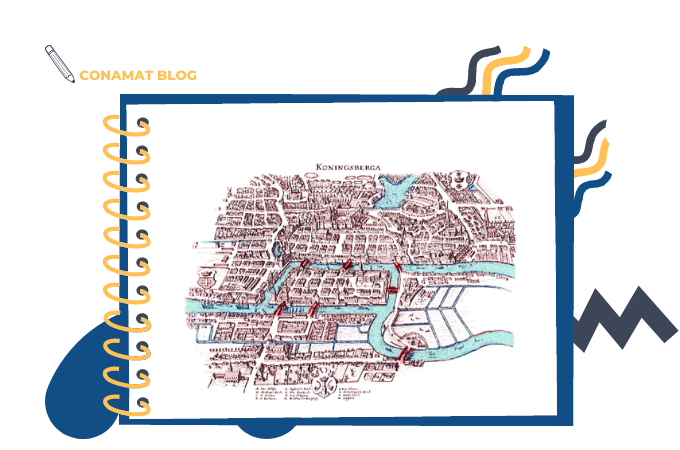
Este último problema dio lugar a la teoría de grafos, una de las ramas de las Matemáticas más interesantes y dinámicas y del cuál hoy aprenderás, de una forma simple, un poco de esta rama.
Para saber si una figura se puede dibujar de un solo trazo sin despegar el lápiz se necesita de nociones básicas, las cuales son:
1. Punto, nodo o vértice par (P)
Es aquel en el cual se unen un número par (P) de rectas o curvas.
.png?width=680&name=Figuras%20con%20v%C3%A9rtices%20o%20puntos%20pares%20(con%20trazos).png)
Figuras con vértices o puntos pares.
2. Punto, nodo o vértice impar (I)
Es aquel en el cual se unen un número impar (I) de rectas o curvas.
.png?width=680&name=Figuras%20con%20v%C3%A9rtices%20o%20puntos%20impares%20(con%20trazos).png)
Con la ayuda de lo anterior para que una figura se pueda dibujar de un solo trazo continúo, sin pasar por 2 o más veces por un mismo trazo, ni levantar el lápiz se debe tomar en cuenta lo siguiente:
Es aquel en el cual, dada una figura todos sus vértices o puntos son pares y, además, SI SE PUEDE DIBUJAR de un solo trazo. La característica de este ciclo es que se elige para iniciar el trazo cualquier punto y en ese mismo punto se termina.
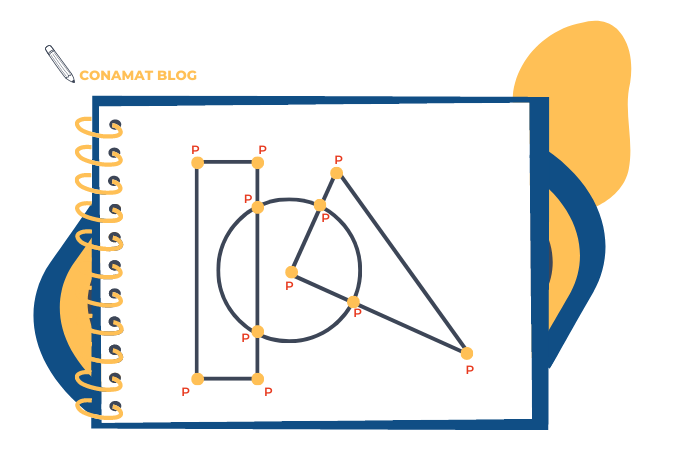
Es aquel en el cual, dada una figura se tienen sólo 2 vértices o puntos impares y, además, SI SE PUEDE DIBUJAR de un solo trazo. La característica de este recorrido es que se elige para iniciar el trazo cualquier punto impar y se terminará en el otro punto o vértice impar.
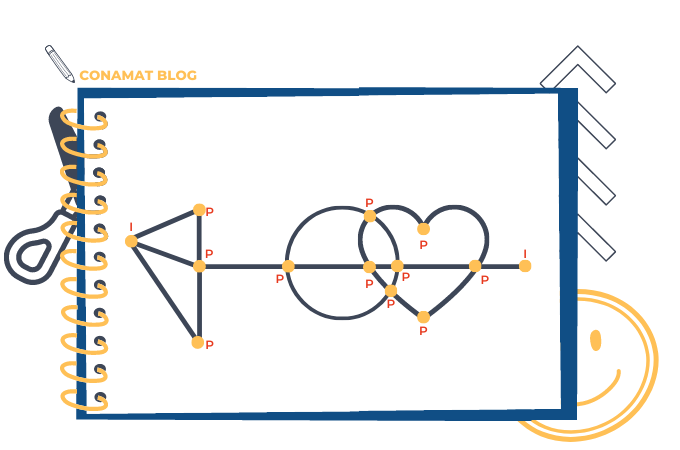
Observa la siguiente imagen, en ella se aprecia que hay 4 vértices o puntos impares, por tal razón Euler dice que no se puede dibujar de un solo trazo sin pasar 2 o más veces por la misma línea y sin despegar el lápiz ya que no es un ciclo Euleriano o un recorrido Euleriano.
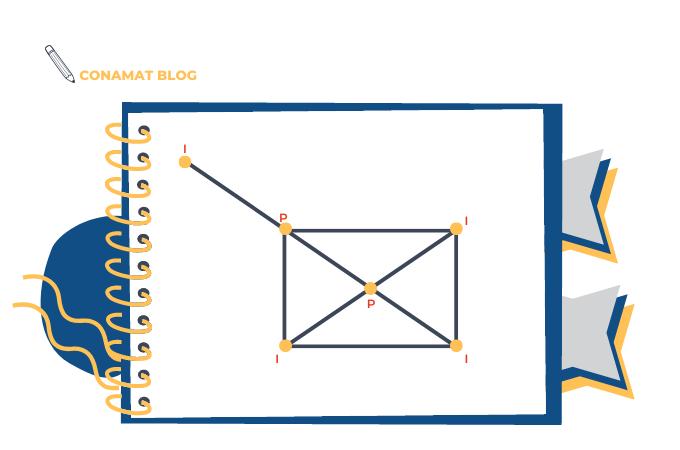
No se puede realizar de un solo trazo ya que son más de dos puntos o vértices impares. Figuras con más de dos vértices o puntos impares.
Esta última figura es lo que tu necesitas para saber si el reto es posible. Por lo tanto, si en una figura se tiene MÁS DE 2 VÉRTICES O PUNTOS IMPARES, es IMPOSIBLE CONSTRUIRLA DE UN SÓLO TRAZO Y NO PASAR MÁS DE UNA SOLA VEZ POR LA MISMA LÍNEA.
Te reto a que dibujes sin despegar el lápiz y sin pasar 2 o más veces por la misma línea el ciclo y recorrido Euleriano antes mostrados.
Para terminar este aprendizaje te comparto una imagen que Euler construyó, dando solución al problema de los 7 puentes de Königsberg, un problema en el que se buscaba pasar una sola vez por todos los puentes y regresando al mismo punto de inicio sin pasar 2 o más veces por el mismo lugar.
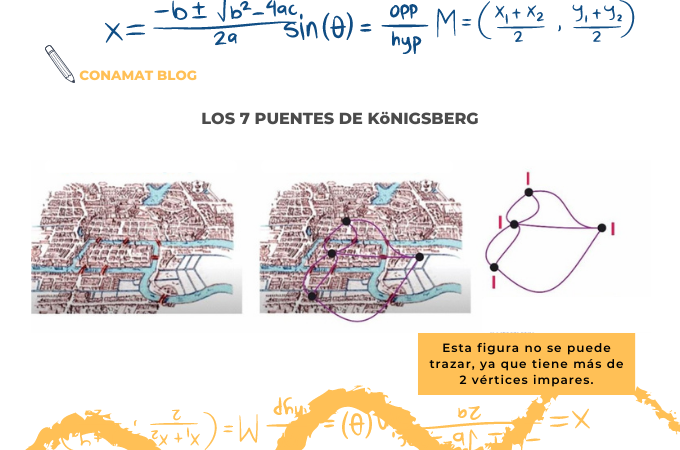7 puentes de Königsberg.Con el trazo de unas cuantas líneas y creatividad nacen bellas figuras.
Los circuitos y recorridos Eulerianos es una muy pequeña parte de la teoría de grafos, pero esta pequeña parte es una introducción básica al mundo de la habilidad o razonamiento matemáticos, especialmente en el tema de “Imaginación espacial”. Uno de los temas más importantes en los contenidos temáticos de los exámenes de ingreso tanto a nivel bachillerato como universitario, por lo que su dominio te permitiría poder ingresar a tu bachillerato y universidad que tú elijas.
¡Queremos escucharte!
Escríbenos un comentario